What are the odds of a solo win in Mexican bingo? (Riddler 2022-10-21)
Published:
My solution to this week’s riddler. (See more of my Riddler solutions here.)
The Problem
From Roberto Linares comes a puzzle that will have you shouting “Bingo!”:
A thousand people are playing Lotería, also known as Mexican bingo. The game consists of a deck of 54 cards, each with a unique picture. Each player has a board with 16 of the 54 pictures, arranged in a 4-by-4 grid. The boards are randomly generated, such that each board has 16 distinct pictures that are equally likely to be any of the 54.
During the game, one card from the deck is drawn at a time, and anyone whose board includes that card’s picture marks it on their board. A player wins by marking four pictures that form one of four patterns, as exemplified below: any entire row, any entire column, the four corners of the grid and any 2-by-2 square.
Four four-by-four grids are shown. In the first grid, the third row has four blue markers. In the second grid, the second column has four blue markers. In the third grid, the four corner squares are marked. And in the fourth grid, the two middle squares in the third and fourth columns are marked, forming a smaller two-by-two square.
After the fourth card has been drawn, there are no winners. What is the probability that there will be exactly one winner when the fifth card is drawn?
The Solution
This is a pretty simple counting and probability problem. Let $p_4$ and $p_5$ be the probabilities that a given board wins after exactly $4$ or $5$ draws, respectively. The probability that we are seeking is therefore
\[P = \operatorname{Pr}\big(\text{exactly one winner after 5 draws }\big|\text{ no winners after 4 draws}\big) = \frac{1000p_5(1-p_4-p_5)^{999}}{(1-p_4)^{1000}}\]It remains to determine $p_4$ and $p_5$. The total number of ways that the first 4 cards can be drawn is simply equal to
\[n_4 = 54\cdot53\cdot52\cdot 51.\]For a given board, we can count the number of ways in which the first 4 cards can be drawn that lead to that board winning as follows. First note that there are 18 distinct winning patterns:
- 4 distinct columns
- 4 distinct rows
- 9 distinct 2x2 blocks
- 1 set of all four corners
To count the number of ways in which a board wins after 4 draws, first pick one of the 18 distinct ways in which that board can win. For the board to win with that pattern, the cards with the four pictures on the four squares composing that pattern must be the first 4 cards that are drawn, in any possible order. Hence there are $18\cdot 4!$ ways that the first 4 cards can be drawn that lead to a given board winning, and thus
\[p_4 = \frac{18\cdot 4!}{54\cdot53\cdot52\cdot 51} = \frac{2}{35139} \approx 0.000056916.\]The number of ways that a board can win after exactly 5 draws is exactly 4 times the number of boards that win after exactly 4 draws. That is,
\[p_5 = 4p_4.\]To see this, note that after 5 draws any valid board can only have at most one of the 18 winning patterns completely filled in. As above, to count the number of ways that a board wins after 5 draws, first pick one of the 18 distinct patterns from above. Of the first 4 cards drawn, exactly one of them cannot match a picture in the four squares comprising the winning pattern (and there are 4 ways this can happen). The 4 cards that do match the pictures in the winning pattern can otherwise be drawn in any order, and thus
\[p_5 = 18\cdot 4\cdot 4! = 4p_4.\]The probability in question can therefore be computed as
\[P = \frac{1000(4p)(1-5p)^{999}}{(1-p)^{1000}} = 0.1813563126414745,\]where $p=p_4 = 2/35139$. Thus the odds of having exactly one winner after the fifth draw, given that there are 1000 players and no winners after the fourth draw, is about 18.1%.
More players? More winners?
What happens when there are more players? Does this probability go up or down?
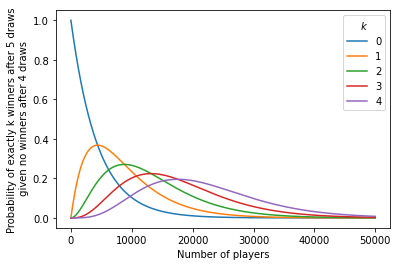
Let $N$ be the number of players (where $N=1000$ in the original problem statement), each with a randomly selected board. The probability that there are exactly $k$ winners after 5 draws given that there were no winners after 4 draws is computed as
\[\begin{align*} \operatorname{Pr}&\big(\text{exactly }k\text{ winners after 5 draws }\big|\text{ no winners after 4 draws}\big)\\ &= \frac{\binom{N}{k}(4p)^k(1-5p)^{N-k}}{(1-p)^{N}} \end{align*}\]As the number of players grows, this probability increases to roughly 36.8% at $N=4293$, after which this probability starts to shrink (the probability of there being multiple winners begins to outstrip the probability of there being exactly one winner). The plot below shows the probabilities of having exactly $k$ winners after the fifth draw as the number $N$ of participants grows, given that there are no winners after the fourth draw.